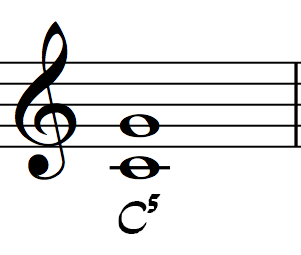A chord is a harmonic structure usually consisting of more than 2 notes being played at the same time. Chords are derived from scales.
- Chords have a root, a type, and a quality.
- A chord’s root is the note that serves as the point of reference for all of its comprising intervals.
- A chord’s type refers to the list of interval distances that determine which notes from the scale are used to build the chord. (ex. the chord type “Triad” = Root, 3rd, 5th)
- A chord’s quality refers to the unique set of specific intervals that make up a chord (determined when a chord’s type is applied to a particular scale) (ex. the chord quality “major triad” = Root, M3, P5)
- The most common chords are derived using the concept of tertian or tertiary harmony, which involves “stacking” notes from a scale in diatonic 3rds starting from the root.
- Diatonic refers to pitches, intervals, or chords that are derived from of a source scale.
Triads #
A triad is the most common chord type found in Western music. It consists of a root with 2 consecutively stacked 3rds. While tertian chords are derived by stacking a scale as a series of consecutive 3rds, they can be more easily understood as a list where each note in the chord is named by its intervallic distance from the chord’s root.
Example: Let’s use the C Lydian scale (C, D, E, F#, G, A B) to build tertian chords:
First, let’s stack two 3rds on top of each other. If we look at each note in relationship to the root, we have a 3rd and a 5th. This forms the most common chord type, the triad. Specifically, we have the intervals M3 and P5, which combined with the root form a major triad.

Triad Qualities
Major – (R, M3, P5)

Minor – (R, m3, P5)

Diminished – (R, m3, d5)

Seventh Chords
If we continue to stack another 3rd on top of a triad, we get a new chord type, the Seventh Chord. (It is important to note that Seventh Chords have 4 notes, and get their name from the new note that is stacked on top of its triad base, which forms the intervallic distance of a 7th from the chord’s root.)

Seventh Chord Qualities
| Name | Chord Symbol | Formula | Shorthand |
|---|---|---|---|
| “Major 7” | maj7, △7, M7 | R, M3, P5, M7 | R, 3, 5, 7 |
| “Minor 7” | min7, -7, m7 | R, m3, P5, m7 | R, ♭3, 5, 7 |
| “Dominant 7” | 7, dom7 | R, M3, P5, m7 | R, 3, 5, ♭7 |
| “Minor 7♭5”, “half diminished” | m7♭5, ø7 | R, m3, d5, m7 | R, ♭3, ♭5, ♭7 |
| “Diminished 7” | dim7, °7 | R, m3, d5, d7 | R, ♭3, ♭5, ♭♭7 |
| “Minor Major 7” | minMaj7, -maj7, min△7 | R, m3, P5, M7 | R, ♭3, 5, 7 |
| “Major 7#5” | maj7#5, maj7+5,△7+5 | R, M3, A5, M7 | R, 3, #5, 7 |
| “Dominant 7#5” | 7#5, 7+5 | R, M3, A5, m7 | R, 3, #5, ♭7 |
| “Dominant 7♭5” | 7♭5 | R, M3, d5, m7 | R, 3, ♭5, ♭7 |
| “Major 7b5” | maj7♭5, △7♭5 | R, M3, d5, M7 | R, 3, ♭5, 7 |
| “Dominant 7sus4” (non-tertian) | 7sus4 | R, P4, P5, m7 | R, 4, 5, ♭7 |

Tensions
When building tertian chords, the R, 3, 5, & 7 are referred to as chord tones. If we continue to stack 3rds beyond the chord’s 7th, we introduce tensions, (also called extensions).
Tensions are the intervals within a chord that are known for their “colorful” dissonance.

Tensions are named 9, 11, & 13 respectively because of their derived origin of stacked 3rds.
9 (scale degree 2 up an octave)
11 (scale degree 4 up an octave)
13 (scale degree 6 up an octave)
Tensions may be # or ♭ depending on the scale they come from.
List of all tensions: ♭9, 9, #9, 11, #11, ♭13, 13
Let’s continue to stack 3rds until we run out of notes in the C Lydian Scale (we eventually circle back to C) C, E, G, B, D, F#, A
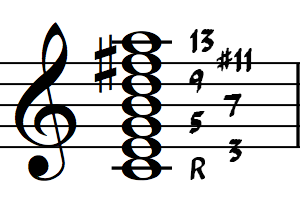
To name a chord quality that uses tensions, it is typical to take the name of the 7th chord quality, and put the tensions in parenthesis. ex. Cmaj7(9,#11,13)
The chord qualities add9, add11, add13 can be used to imply that the 7th of the chord is omitted. (Cadd9, Fadd#11)

Adding (no3, no5, etc) to the chord quality can be used to specifically indicate which chord members are omitted.
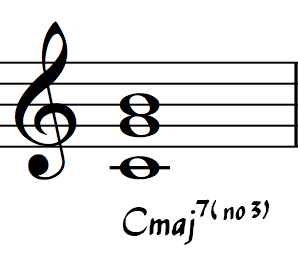
Chord-Scale
A chord-scale is the representation of a scale so that each of scale note is named in accordance with its chordal function (chord tone or tension).

While tensions certainly do add a sense of yearning for resolution, depending on the scale, some 9’s, 11’s, and 13’s result in highly dissonant or unstable chord structures. (more than their inherent dissonance as being a chord’s 9th, 11th , or 13th) These notes instead are referred to as avoid notes, and are usually more suitable to be used as passing tones in a melodic phrase than to establish a harmonic progression. Some scales have no avoid notes – others have more than 1.

Power Chords are simply a root and a perfect fifth.