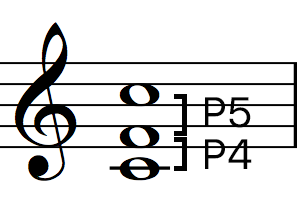Intervals are the building blocks that make up scales and chords.
An interval represents the “musical distance” between 2 notes and consists of both a distance and a type.
An interval’s distance is the number of letters in the musical alphabet between the starting letter and the ending letter (include both the starting and ending letter). Sharps (#) and flats (♭) are irrelevant in determining the distance – but will be necessary to identify the interval’s type.
Example: What is the interval distance between C and G#?
C, D, E, F, G = 5 letters This interval has the distance of a 5th.
Distances:
| Unison | (ex. C→ C, the musical distance of 0) |
| 2nd | (ex. C → D) |
| 3rd | (ex. C → E) |
| 4th | (ex. C → F) |
| 5th | (ex. C → G) |
| 6th | (ex. C → A) |
| 7th | (ex. C → B) |
| Octave | (ex. C → C above) |
We can get even more specific by identifying the interval’s type, the aspect of an interval that describes its behavior when raising or lowering it. There are 5 interval types:
Types:
Perfect (P)
Major (M)
Minor (m)
Augmented (A or +)
Diminished (d or °)
Types can most easily be described using the C major scale as an example. (C, D, E, F, G, A, & B)
Let’s start by writing the C major scale as a series of interval distances in relationship to the root:
| Concrete | Abstract |
| C → C | Unison |
| C → D | 2nd |
| C → E | 3rd |
| C → F | 4th |
| C → G | 5th |
| C → A | 6th |
| C → B | 7th |
| C → C | Octave |
In any major scale:
- Unisons, 4ths, 5ths, and Octaves are Perfect (their type)
- Every other interval is Major (2nd, 3rd, 6th, & 7th)
We can abbreviate each specific interval by the letter of its type (P, M, m, A, d) then the number from its distance (1, 2, 3, etc.)
| Concrete | Abstract |
| C → C | P1 |
| C → D | M2 |
| C → E | M3 |
| C → F | P4 |
| C → G | P5 |
| C → A | M6 |
| C → B | M7 |
| C → C | P8 |
The major scale can be written as a list of specific intervals in reference to a common root: P1, M2, M3, P4, P5, M6, M7, P8
We can further simplify this list by removing the outer values, as P1 and P8 exist in every conceivable scale.
M2, M3, P4, P5, M6, M7
Interval Type Behavior
So we can successfully identify any specific interval in the C major scale – Great! But what if we want to know the interval of C to E♭, or C to F#, or C to any # or ♭ for that matter?
Let’s take a closer look at how perfect and major intervals behave when we start raising or lowering them.
| augmented (A) | augmented (A) |
| ⇅ | ⇅ |
| perfect (P) | major (M) |
| ⇅ | ⇅ |
| diminished (d) | minor (m) |
| ⇅ | |
| diminished (d) |
Perfect intervals (P) become augmented (A) when raised by a semitone and diminished (d) when lowered by a semitone.
Major intervals (M) also become augmented (A) when raised by a semitone but become minor (m) when lowered by a semitone. If a minor interval is lowered, it then becomes diminished (d).
What interval is C→E♭?
Taking our knowledge of the intervals in the C major scale, we know that C→ E is a major 3rd (M3). E♭ is a half step lower than E, so we need to lower the M3 interval to identify C→ E♭. Major intervals when lowered become minor, therefore C→ E♭ is a minor 3rd (m3).
What interval is C→F#?
Also utilizing our knowledge of the intervals in the C major scale, we know that C→ F is a perfect 4th (P4). F# is a half step above F, so we need to raise the P4 interval to identify C→ F#. Perfect intervals when raised become augmented, therefore C→ F# is an augmented 4th (A4).
Pitches can be referred to using different names, called enharmonic spellings.
For example, the black keys on the piano can each be given a sharp (#) and a flat (♭) name:
C# = D♭
D# = E♭
F# = G♭
G# = A♭
A# = B♭
While C# and D♭ have the same pitch. their respective spellings have different implications on how an interval is named.
Example:
C→D# is an augmented 2nd (A2).
C→E♭ is a minor 3rd (m3).
Although an A2 and m3 will sound exactly the same, their functions differ. This distinction will become less trivial as we start constructing chords, which require specific interval formulas.
At this point, we should have all the tools needed to identify any specific interval using C as the root. But what about identifying intervals in reference to any other root? This process is a little more involved, and requires familiarization with key signatures, which can be learned by studying the Circle of Fifths.
Already know key signatures? Great – let’s apply our knowledge to start building more intervals!
Example: What interval is E→D?
- Let’s make a list of each interval in the major scale of the interval’s root (E). Let’s also indicate each major scale degree’s respective interval.
| Concrete | Abstract |
| E → E | P1 |
| E → F# | M2 |
| E → G# | M3 |
| E → A | P4 |
| E → B | P5 |
| E → C# | M6 |
| E → D# | M7 |
| E → E | P8 |
- Since we are trying to solve for D, find the pitch in the E major scale with that letter (D#). D# is a M7. D is a half-step lower than D#, so we need to lower the M7 interval. Major intervals when lowered become minor, therefore E→D is a minor 7th (m7)
Alternative Method
There is an alternative method to accurately derive specific intervals without knowledge of key signatures.
Example: What interval is D♭→G?
Find interval distance between the letters (remember to ignore #’s and ♭’s)
Count the number of semitones (half-steps) between both pitches (pay attention to #’s and ♭’s)
D♭→G = 6 semitones
Find the match in the list below between the distance number in step 1 and the number of semitones.
Intervals values in Semitones
m2 = 1
M2 = 2
A2 = 3
m3 = 3
M3 = 4
d4 = 4
P4 = 5
A4 = 6
d5 = 6
P5 = 7
A5 = 8
m6 = 8
M6 = 9
d7 = 9
m7 = 10
M7 = 11
Compound Intervals (Intervals Larger than 1 Octave)
Intervals continue to be given names up to 2 octaves (anything above which are typically referred to by their function within a chord or scales instead of continuing to extend the interval distance.)
Intervals stretching above an octave directly mimic the type of the interval an octave directly below them. As such the following list can be used to show the synonymous relationship between interval types
9ths = 2nds
10ths = 3rds
11ths = 4ths
12ths = 5ths
13ths = 6ths
14ths = 7ths
Interval Inversions
An interval becomes inverted when the 2 notes of the interval swap locations
C to F = P4
F to C = P5
The sum of an interval and its inversion will always equal an octave.
Below is a list of Generic Interval Inversion pairs:
2nds / 7ths
3rds / 6ths
4ths / 5ths
5ths / 4ths
6ths / 3rds
7ths / 2nds
Below is a list of Specific Interval Inversions pairs:
2nds / 7ths
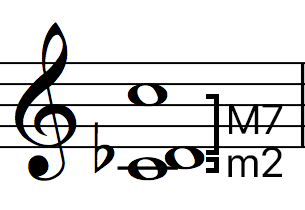
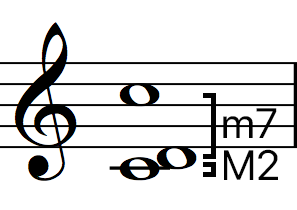


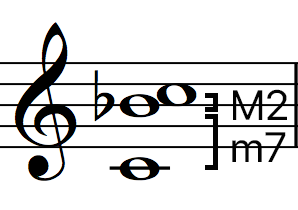
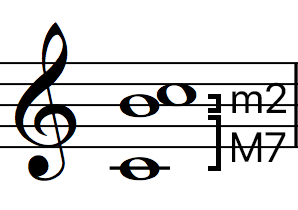
3rds / 6ths
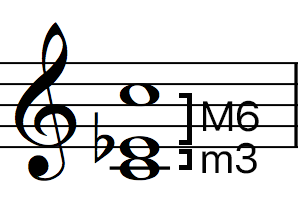
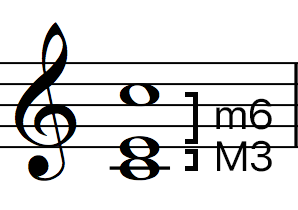


4ths / 5ths